(author: John Salatas)
Foreword
This article is the first part of a series of articles on porting openFST[1] in java. OpenFST is an open-source C++ library for weighted finite-state transducers (WFSTs) [1] and having a similar java implementation is a crucial first step for the integration of phonetisaurus g2p into sphinx 4 [2]
This article will briefly review some mathematical background of weighted finite-state transducers describe the current implementation of openFST and then start describing the java implementation which will be completed in articles that will follow.
1. Weighted finite-state transducers
Weighted finite-state transducers have been used in speech recognition and synthesis, machine translation, optical character recognition, pattern matching,string processing, machine learning, information extraction and retrieval among others. Having a comprehensive software library of weighted transducer representations and core algorithms is key for using weighted transducers in these applications and for the development of new algorithms and applications. [1]
A weighted finite-state transducer (WFST) is a finite automaton for which each transition has an input label, an output label, and a weight. Figure 1 depicts a weighted finite state transducer: [1]
[caption id="attachment_339" align="aligncenter" width="497" caption="Figure 1: Example weighted finite-state transducer"]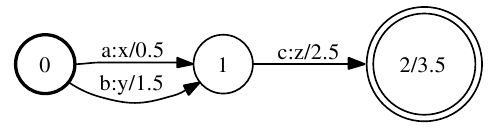
[/caption]
The initial state is labeled 0. The final state is 2 with final weight of 3.5. Any state with non-infinite final weight is a final state. There is a transition from state 0 to 1 with input label a, output label x, and weight 0.5. This machine transduces, for instance, the string ac to xz with weight 6.5 (the sum of the arc and final weights). [1]
The weights may represent any set so long as they form a semiring. A semiring $latex (\mathbb{K}, \oplus, \otimes, \bar{0}, \bar{1}) $ is specified by a set of values $latex \mathbb{K} $, two binary operations $latex \oplus $ and $latex \otimes $, and two designated values $latex \bar{0} $ and $latex \bar{1} $. The operation $latex \oplus $ is associative, commutative, and has $latex \bar{0} $ as identity. The operation $latex \otimes $ is associative, has identity $ and $latex \bar{1} $, distributes with respect to $latex \oplus $, and has $latex \bar{0} $ as annihilator: for all $latex a \in \mathbb{K} , a \otimes \bar{0} = \bar{0} \otimes a = \bar{0} $. If $latex \otimes $ is also commutative, we say that the semiring is commutative. [1]
Table 1 below lists some common semirings. All but the last are defined over subsets of the real numbers (extended with positive and negative infinity). In addition to the familiar Boolean semiring, and the probability semiring used to combine probabilities, two semirings often used in applications are the log semiring which is isomorphic to the probability semiring via the negative-log mapping, and the tropical semiring which is similar to the log semiring except the operation is min. The left (right) string semiring, which is defined over strings, has longest common prefix (suffix) and concatenation as its operations, and has the (extended element) infinite string and the empty string for its identity elements. It only distributes on the left (right). [1]
[caption id="attachment_355" align="aligncenter" width="347" caption="Table 1: Semiring examples."]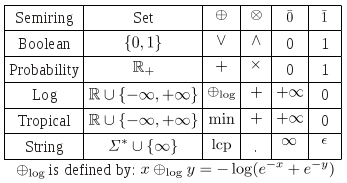
[/caption]
2. The openFST C++ library: Representation and Construction
The motivation for OpenFst was to create a library as comprehensive and efficient as the AT&T FSM [3] Library, but that was an open-source project. We also sought to make this library as flexible and customizable as possible given the wide range of applications WFSTs have enjoyed in recent years. It is a C++ template library, allowing it to be both very customizable and efficient. [1]
In the OpenFst Library, a transducer can be constructed from either the C++ level using class constructors and mutators or from a shell-level program using a textual file representation. [1]
In order to create a transducer using openFST we need first to construct an empty VectorFst: [1]
// A vector FST is a general mutable FST
VectorFst fst;
The VectorFst, like all transducer representations and algorithms in this library, is templated on the transition type. This permits customization of the labels, state IDs and weights in a transducer. StdArc defines the library-standard transition representation:
template
class ArcTpl {
public:
typedef W Weight;
typedef int Label;
typedef int StateId;
ArcTpl(Label i, Label o, const Weight& w, StateId s)
: ilabel(i), olabel(o), weight(w), nextstate(s) {}
ArcTpl() {}
static const string &Type(void) {
static const string type =
(Weight::Type() == "tropical") ? "standard" : Weight::Type();
return type;
}
Label ilabel;
Label olabel;
Weight weight;
StateId nextstate;
};
A Weight class holds the set element and provides the semiring operations. Currently openFST provides many different C++ Template-based implementations like TropicalWeightTpl, LogWeightTpl and MinMaxWeightTpl which extend a base FloatWeightTpl (see float-weight.h for implementation details) and others. Having these Template-based implementations opeFST we need just have a typedef to define a particular Weight such as TropicalWeight:
// Single precision tropical weight
typedef TropicalWeightTpl TropicalWeight;
3. The proposed FST java library
Based on the above description and on technical implementation differences between C++ and Java, and more specific mostly on a) difference between C++ Templates and Java generics [4] and b) the lack of operation overloads in Java, the initial implementation includes the edu.cmu.sphinx.fst.weight.Weight
There is also a generics based interface edu.cmu.sphinx.fst.weight.Semiring
Finaly the edu.cmu.sphinx.fst.demos.basic package contains a main class for testing the above functionality by instatiating a TropicalSemiring and performing some operations on various Weight values.
4. Conclusion – Future work
This article tried to describe some basic theoritical background on weighted finite-state transducers, provide a brief description on the openFST architect and foundation classes and finally presented an initial design for the FST java library implementation. Following the general open-source philosophy “perform small commits often” the library is available in CMUShinx' repository created for the integration of phonetisaurus g2p into sphinx 4. [5]
The next steps is to provide the Arc and Fst classes which over time will be extended to provide the required functionality for the various FST operations needed for my GSoC 2012 project. Hopefully, over time, more functionality will be provided by the community.
References
[1] C. Allauzen, M. Riley, J. Schalkwyk, W. Skut, M. Mohri, “OpenFst: a general and efficient weighted finite-state transducer library”, Proceedings of the 12th International Conference on Implementation and Application of Automata (CIAA 2007), pp. 11–23, Prague, Czech Republic, July 2007.
[2] J. Salatas, “Phonetisaurus: A WFST-driven Phoneticizer – Framework Review”, last accessed: 08/05/2012.
[3] M. Mohri, F. Pereira, M. Riley, “The Design Principles of a Weighted Finite-State Transducer Library”, Theoretical Computer Science, pp. 15-32, 2000.
[4] H. M. Qusay, “Using and Programming Generics in J2SE 5.0”, Oracle Technology Network, 2004, last accessed: 08/05/2012.